regola carattere

statistica descittiva

indici di variabilità

campo di variazione
gli scarti
scarto sempl. mediano
scarto semplice medio
varianza
deviazione standard
coefficiente di variaz.

indici di variabilità

Gli indici di variabilità (detti anche indici di dispersione) sono quegli strumenti che consontono di misurare la variabilità di una distribuzione statistica quantitativa.

In sostanza ci indicano quanto differiscano tra loro un insieme di valori numerici.

Volendo sintetizzare un insieme di modalità si possono usare una o più medie, ma la descrizione risulterebbe sommaria se non andassimo a quantificare la variabilità dell'insieme in esame.

Nel caso di modalità tutte uguali fra loro, ovvero di variabilità nulla, tutti gli indici di variabilità produrranno zero, ma maggiore sarà la diversità tra le modalità, maggiori saranno i valori ricavati come indici di variabilità.

Partiamo da un esempio:

Si immagini un gioco a premi che si svolga da 10 anni e preveda i seguenti premi:

estratto	€
1º	1000
2º	200
3º	100

Aggiungiamo che ogni anno, siano stati stampati e venduti 100 biglietti per partecipare al gioco.

Ora ci si chiede:

qual'è la vincita media dei primi classificati di tutti i 10 anni?
qual'e la vincita media dei tre premiati?
qual'è la vincita media dei partecipanti dell'ultimo anno?

Le risposte saranno:

$\bar{x} = \frac{1000 \cdot 10}{10} = 1000 €$
$\bar{x} = \frac{1000 + 200 + 100}{3} = \frac{1300}{3} = 433 . \bar{3} €$
$\bar{x} = \frac{1000 \cdot 1 + 200 \cdot 1 + 100 \cdot 1 + 0 \cdot 97}{100} = \frac{1300}{100} = 13 €$

Come si vede, nel primo caso la media formirsce un valore estremamente significativo, meno nel secondo e per il terzo, la media fornisce una sintesi assai poco indicativa, infatti, come evidenziato parlando della media aritmetica, essa perde di significato all'aumentare della variabilità dei valori sintetizzati.

Sia per determinare la significatività della media aritmetica, sia in generale, ovvero per descrivere meglio un insieme di valori numerici, vediamo come si misura la variabilità di una distribuzione statistica.

In generale distinguiamo tra indici di variabilità assoluti e relativi:

indici di variabilità
assoluti	relativi
campo di variazione	coefficiente di variazione
scarto semplice mediano
scarto semplice medio
varianza
deviazione standard (o scarto quadratico medio)

gli indici di variabilità assoluti sono espressi con la medesima unità di misura delle modalità (per la varianza al quadrato).
gli indici di variabilità relativi sono numeri puri esprimibili in percentuale.

campo di variazione

il campo di variazione misura l'ampiezza dell'intervallo in cui ricadono tutte le modalità.

Il campo di variazione (detto anche intervallo di variabilità), è la differenza tra il valore massimo e quello minimo. Essendo una differenza, non mi dispiace indicarlo con la lettera greca delta maiuscola (Δ).

formula

campo di variazione

note

Il campo di variazione è un indice di variabilità debole visto che tiene in considerazione soltanto due modalità, la maggiore e la minore, inoltre è suscettibile a valori eccezionali che ne inficiano la significatività.

esempio di campo di variazione

Osservando la spesa giornaliera (in €) di un gruppo di persone si è ricavata la seguente distribuzione unitaria:

x
7
8
10
11
14
16
17
19
20
33

Il campo di variazione si calcola così:

$Δ = x_{m a x} - x_{m i n} = 33 - 7 = 26 €$

Ovvero le modalità ricadono tutte in un intervallo di 26€, ma graficamente:

campo di variazione

si nota meglio che la modalità 33€, in quanto eccezionale porta il campo di variazione da 13€ (20 - 7) a 26€ pregiudicandone la significatività.

Si aggiunga che se le 10 modalità fossero state tutte 7€ esclusa una a 33€, oppure tutte 33€ esclusa una a 7€, il campo di variazione sarebbe stato sempre 26€.

nota

Si rimanda ad altra fonte la trattazione del più stabile campo di variazione interquartile.

gli scarti

Per ottenere un indice di variabilità che consideri tutte le modalità, ci si riferisce ai loro scarti da un indice di posizione centrale.

Con scarto (detto anche deviazione o scostamento) intendiamo la distanza che separa ciascuno dei dati da un medesimo valore centrale che di norma è la loro media aritmetica.

Disponendo di n modalità, otterremo n scarti, visto che ciascuna modalità si scosta dalla media di una quantità pari alla loro differenza:

scarto = x - media.

A questo punto, tutti i valori inferiori alla media avranno uno scarto negativo e tutti gli altri uno positivo.

Portando ad esempio la seguente distribuzione unitaria che riporta il numero di promossi in dieci sessioni di uno stesso esame:

sessione	promossi
1ª	12
2ª	9
3ª	10
4ª	14
5ª	16
6ª	18
7ª	16
8ª	10
9ª	18
10ª	17
Σ	140

Lla media aritmetica dei promossi, si ottiene $\frac{140}{10} = 14 promossi$ ; si calcolano quindi gli scarti così:

x	scarto
12	12 - 14 = -2
9	9 - 14 = -5
10	10 - 14 = -4
14	14 - 14 = 0
16	16 - 14 = 2
18	18 - 14 = 4
16	16 - 14 = 2
10	10 - 14 = -4
18	18 - 14 = 4
17	17 - 14 = 3
Σ	0

Ricordando infatti che la media aritmetica è quel valore che se sostituito ai dati produce la stessa somma, è facilmente dimostrabile che la somma degli scarti relativi è nulla:

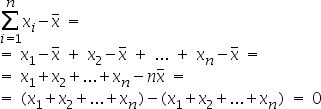
dimostrazione somma nulla degli scarti relativi

proprietà delle medie rispetto agli scarti

Si ricorda che per le proprietà della mediana, calcolando gli scarti rispetto ad essa, la somma dei loro valori assoluti è la minore possibile, ma si rimanda ad altra fonte la trattazione completa dello scarto semplice mediano, il quale trova scarso utilizzo in quanto la mediana, essendo una media di posizione, non considera tutti i dati a disposizione, ma soltanto quello/la coppia centrale.
Come appena dimostrato, per le proprietà della media aritmetica la somma degli scarti relativi (dalla media), la loro somma è nulla.
Si ricorda che, sempre per le proprietà della media aritmetica la somma degli scarti al quadrato (dalla media), la loro somma è la minore possibile.

scarto semplice medio

Come appena precisato parlando degli scarti dalla media, essendo nulla la loro somma è ovviamente nulla anche la loro media, ergo, lo scarto semplice medio relativo è un valore nullo per le proprietà della media aritmetica.

Considerando però gli scarti in valore assoluto otterremo lo scarto (o scostamento) semplice medio.

In sostanza è la media aritmetica degli scarti assoluti.

formula

semplice	ponderato

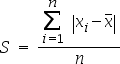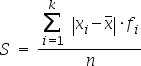esempio di scarto semplice medio semplice

Portiamo ad esempio la distribuzione unitaria vista sopra riguardante il numero di promossi in dieci sessioni di un medesimo esame:

sessione	promossi
1ª	12
2ª	9
3ª	10
4ª	14
5ª	16
6ª	18
7ª	16
8ª	10
9ª	18
10ª	17
Σ	140

Essendo la media di 10 promossi, calcoliamo lo scarto semplice medio assoluto così:

sessione	promossi	scarto relativo	scarto assoluto
1ª	12	12 - 14 = -2	\|12 - 14\| = 2
2ª	9	9 - 14 = -5	\|9 - 14\| = 5
3ª	10	10 - 14 = -4	\|10 - 14\| = 4
4ª	14	14 - 14 = 0	\|14 - 14\| = 0
5ª	16	16 - 14 = 2	\|16 - 14\| = 2
6ª	18	18 - 14 = 4	\|18 - 14\| = 4
7ª	16	16 - 14 = 2	\|16 - 14\| = 2
8ª	10	10 - 14 = -4	\|10 - 14\| = 4
9ª	18	18 - 14 = 4	\|18 - 14\| = 4
10ª	17	17 - 14 = 3	\|17 - 14\| = 3
Σ	140	0	30

Quindi lo scarto semplice medio assoluto, vale $\frac{30}{10} = 3 promossi$

Applicando la formula:

$\begin{array}{l} S = \frac{\sum_{i = 1}^{n} | x_{i} - \bar{x} |}{n} = \frac{| x_{1} - \bar{x} | + | x_{2} - \bar{x} | + . . . + | x_{n} - \bar{x} |}{n} = \\ = \frac{| 12 - 14 | + | 9 - 14 | + | 10 - 14 | + | 14 - 14 | + | 16 - 14 | + | 18 - 14 | + | 16 - 14 | + | 10 - 14 | + | 18 - 14 | + | 17 - 14 |}{10} = \\ = \frac{| - 2 | + | - 5 | + | - 4 | + | 0 | + | 2 | + | 4 | + | 2 | + | - 4 | + | 4 | + | 3 |}{10} = \\ = \frac{2 + 5 + 4 + 0 + 2 + 4 + 2 + 4 + 4 + 3}{10} = \frac{30}{10} = 3 p \end{array}$